
Figure 1 Unstructured Mesh
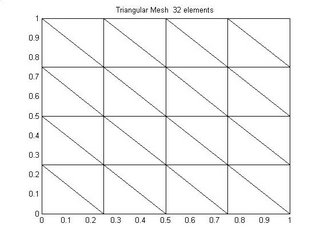
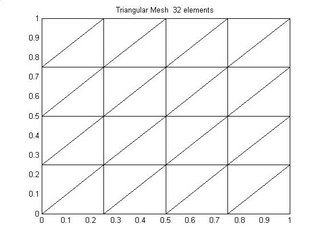
Triangular meshs can also be structured triangular with triangulation in some particular direction as shown in figure 2 and figure 3.
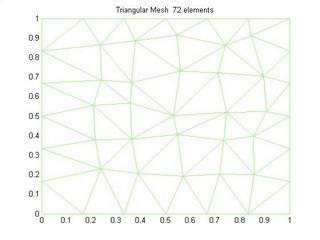
The Unstructured mesh shown in Figure 1 is basically made by randomly perturbing the nodes of a unifrom triangular mesh and it look very much like a delaunay mesh. Figure 4 shows a unstructured triangular delaunay mesh.
Now comming to How to generate shuch kind of meshes. I will here give a simple example of generating regular structured triangular mesh.
The code below is used to create the above triangular structured mesh
x=[0:1/(numx):1];
y=[0:1/(numy):1]; %Matlab's meshgrid is used to create 2D grid from specified divisons above
[X,Y] = meshgrid(x,y);
X1=reshape(X',length(x)*length(y),1);
Y1=reshape(Y',length(x)*length(y),1); %Coordinates of the node
node=[X1 Y1]; % Node
tri = triangulate(X1,Y1,element); % element connectivity
nele = size(tri,1);
Z= zeros(length(y)-2,length(x)-2);
nn = tri; % nodes in a long list
xx = X1(nn); yy = Y1(nn); % coordinates corresponding to nodes
xplot = reshape(xx,size(tri));
yplot = reshape(yy,size(tri));figure(1);
clf;
fill(xplot',yplot','w');
title(['Triangular Mesh ', num2str(length(nn)),' elements'])
%%%%%%Subfunction % triangulate
function tri = triangulate(xnod,ynod,nodes)
%
% tri = triangulate(xnod,ynod,nodes)
%
% triangulate the quadrilateral mesh
%
nele = size(nodes,1);
tri = zeros(3,2*nele)';
iv = [];
ii1 = [2 3 1];
jj1 = [4 1 3];
ii2 = [1 2 4];
jj2 = [2 3 4];
nrtri = 0;
for iel = 1:nele
iv = nodes(iel,:);
d1 = norm([xnod(iv(1))-xnod(iv(3));ynod(iv(1))-ynod(iv(3))]);
d2 = norm([xnod(iv(2))-xnod(iv(4));ynod(iv(2))-ynod(iv(4))]);
if d1 <= d2
nrtri = nrtri+1;
tri(nrtri,:) = iv(ii1);
nrtri = nrtri+1;
tri(nrtri,:) = iv(jj1);
else
nrtri = nrtri+1;
tri(nrtri,:) = iv(ii2);
nrtri = nrtri+1;
tri(nrtri,:) = iv(jj2);
end
end
This code will enable any one to generate a regular triangular mesh and different changes can be made to this code to get other kind of Triangular meshes as shown in figure 1 -4