Website moved

Hi all those of you who are interested in my webpage for downloading meshing codes, the site has now been moved to http://pavondea.web.officelive.com/default.aspx

Enjoy browsing.

Cheers

Pavon

Unstructured 2D Triangular Mesh Matlab

Hello all,

For most of the Numerical simulations Unstructured Mesh are most favourable ones. Especially for Finite Element methods triangular delaunay meshes are used quite a lot. Today I am going to descibe about unstructured Mesh generation in MATLAB.

A typical Unstructured mesh in 2D looks like figure 1.

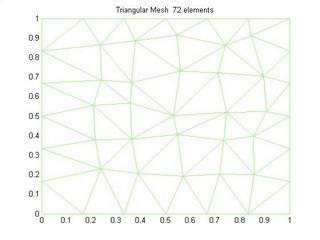
Figure 1 Unstructured Mesh

Triangular meshs can also be structured triangular with triangulation in some particular direction as shown in figure 2 and figure 3.

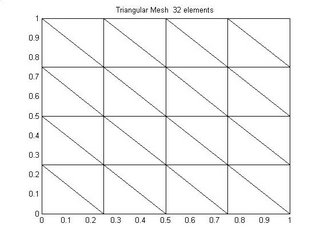
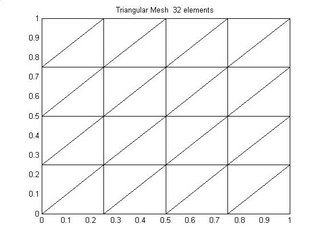
The Unstructured mesh shown in Figure 1 is basically made by randomly perturbing the nodes of a unifrom triangular mesh and it look very much like a delaunay mesh. Figure 4 shows a unstructured triangular delaunay mesh.

Now comming to How to generate shuch kind of meshes. I will here give a simple example of generating regular structured triangular mesh.

The code below is used to create the above triangular structured mesh

x=[0:1/(numx):1];

y=[0:1/(numy):1]; %Matlab's meshgrid is used to create 2D grid from specified divisons above
[X,Y] = meshgrid(x,y);

X1=reshape(X',length(x)*length(y),1);

Y1=reshape(Y',length(x)*length(y),1); %Coordinates of the node

node=[X1 Y1]; % Node
tri = triangulate(X1,Y1,element); % element connectivity

nele = size(tri,1);

Z= zeros(length(y)-2,length(x)-2);

nn = tri; % nodes in a long list

xx = X1(nn); yy = Y1(nn); % coordinates corresponding to nodes

xplot = reshape(xx,size(tri));

yplot = reshape(yy,size(tri));figure(1);

clf;

fill(xplot',yplot','w');

title(['Triangular Mesh ', num2str(length(nn)),' elements'])

%%%%%%Subfunction % triangulate

function tri = triangulate(xnod,ynod,nodes)
%
% tri = triangulate(xnod,ynod,nodes)
%
% triangulate the quadrilateral mesh
%

nele = size(nodes,1);
tri = zeros(3,2*nele)';
iv = [];
ii1 = [2 3 1];
jj1 = [4 1 3];
ii2 = [1 2 4];
jj2 = [2 3 4];
nrtri = 0;
for iel = 1:nele
iv = nodes(iel,:);
d1 = norm([xnod(iv(1))-xnod(iv(3));ynod(iv(1))-ynod(iv(3))]);
d2 = norm([xnod(iv(2))-xnod(iv(4));ynod(iv(2))-ynod(iv(4))]);
if d1 <= d2
nrtri = nrtri+1;
tri(nrtri,:) = iv(ii1);
nrtri = nrtri+1;
tri(nrtri,:) = iv(jj1);
else
nrtri = nrtri+1;
tri(nrtri,:) = iv(ii2);
nrtri = nrtri+1;
tri(nrtri,:) = iv(jj2);
end
end


This code will enable any one to generate a regular triangular mesh and different changes can be made to this code to get other kind of Triangular meshes as shown in figure 1 -4

Mesh Generation Using MATLAB Delaunay Function

If you are using Matlab Delaunay function to generate a unstructured 2D or 3D mesh you will land up in some sort of trouble. For very simple reasons. Have a look at the following piece of MATLAB code.

This code is to generate 3D tetrahedral mesh using the Matlab function Delaunay

x=[(0):1/(numx):(1)]; % numx=numy=numz = 1 (typical cube)

y=[(0):1/(numy):(1)];

z=[(0):1/(numz):(1)];
[X,Y,Z] = meshgrid(x,y,z);

X = [X(:)];

Y= [Y(:)];

Z = [Z(:)];

Tes = delaunay3(X,Y,Z);

L = [X(:) Y(:) Z(:)];

tetramesh1(Tes,L);camorbit(20,0) ;

This gives me a tetrahedral mesh with 'Tes' having the nodal connectivity matrix for a typical case (a cube with 6-tetrahedra, 8 nodes)it looks like

Tes = 4 7 8 6

1 5 7 6

2 4 7 6

2 1 7 6

2 4 7 3

2 1 7 3

Now if you are not care full you might land up in trouble. The reason being that output of delaunay function is in a random order some of the tessellation are arranged in clock wise direction and some in anticlockwise direction. So you need to reorder the tessellation in a particluar oder keeping one/summit node fixed and arranging others in clockwise or anticlcokwise direction.

Same thing happens in 2D. Now you can either do that if you are fond of MATLAB function Delaunay or you can use fowllowing piece of code given to me by some one who is master in tetrahedral meshes.

function [vertices,tess]=tess_lat(varargin)
% tess_lat: simplicial tessellation of a rectangular lattice
% usage: [tessellation,vertices]=tess_lat(p1,p2,p3,...)
%
% arguments: input
% p1,p2,p3,... - numeric vectors defining the lattice in
% each dimension.
% Each vector must be of length >= 1
%
% arguments: (output)
% vertices - factorial lattice created from (p1,p2,p3,...)
% Each row of this array is one node in the lattice
% tess - integer array defining simplexes as references to
% rows of "vertices".


% dimension of the lattice
n = length(varargin);


% create a single n-d hypercube
% list of vertices of the cube itself
vhc=('1'==dec2bin(0:(2^n-1)));
% permutations of the integers 1:n
p=perms(1:n);
nt=factorial(n);
thc=zeros(nt,n+1);
for i=1:nt
thc(i,:)=find(all(diff(vhc(:,p(i,:)),[],2)>=0,2))';
end


% build the complete lattice
nodecount = cellfun('length',varargin);
if any(nodecount<2)
error 'Each dimension must be of size 2 or more.'
end
vertices = lattice(varargin{:});


% unrolled index into each hyper-rectangle in the lattice
ind = cell(1,n);
for i=1:n
ind{i} = 0:(nodecount(i)-2);
end
ind = lattice(ind{:});
k = cumprod([1,nodecount(1:(end-1))]);
ind = 1+ind*k';
nind = length(ind);


offset=vhc*k';
tess=zeros(nt*nind,n+1);
L=(1:nind)';
for i=1:nt
tess(L,:)=repmat(ind,1,n+1)+repmat(offset(thc(i,:))',nind,1);
L=L+nind;
end


% ======== subfunction ========
function g = lattice(varargin)
% generate a factorial lattice in n variables
n=nargin;
sizes = cellfun('length',varargin);
c=cell(1,n);
[c{1:n}]=ndgrid(varargin{:});
g=zeros(prod(sizes),n);
for i=1:n
g(:,i)=c{i}(:);
end

In the next post I will discuss how you can get boundary nodes in a much easier fashion for any kind of meshes by using Faces in 3D.

Element Connectivity for the Hex Mesh : Mesh generation using MATLAB

In the Last post it was defined how to creat a basic Hex mesh in Matlab. What though was missing from the Post was how to get the element connectivity which needs to be Fed to the function which calculates the face connectivity.

So here are few simple steps by which you can easily get the Element Connectivites for the Basic Hexahedral Mesh while using MATLAB.


function element=make_elem(node_pattern,num_u,num_v,num_w,inc_u,inc_v,inc_w,nnx)

%
% Synopsis: element = make_elem(node_pattern,num_u,num_v,num_w,inc_u,inc_v,inc_w,nnx)
%
% Input: node_pattern > Natural node ordering for elements
% node_pattern=[ 1 2 nnx+1 nnx+2 nny+1 nny+2 nny+nnx+1 nny+nnx+2 ]; % Node pattern 1 %2 3 4 5 6 7 8 % according to me notations

% num_u > Number of control volumes in X direction.
% num_v > Number of control volumes in Y direction.
% inc_u > Increment in cell numbers in X direction
% inc_v > Increment in cell numbers in Y direction
%
% Output: element > Element connectivity matrix.


inc=[zeros(1,size(node_pattern,2))];
e=1;
element=zeros(num_u*num_v*num_w,size(node_pattern,2));

for row=1:num_v*num_u
for col=1:num_u
element(e,:)=node_pattern+inc;
inc=inc+inc_u;
e=e+1;
end
inc = row*inc_v;
if mod(e-1,num_u*num_v)==0
node_pattern = node_pattern + nnx;
end
end



% These few simple Steps will help any one who wants to get a basic Hex mesh using MATLAB

Few Tips on Mesh Generation in 3D Using Matlab

3D meshes/girds can be made from different type of mesh elements.

1.) Hexahedral Mesh elements.
2.) Tetrahedral Mesh elements.
3.) Pyramid Shape Mesh elements.
4.) Prism Types of Mesh elements.

Now if you can visualize it is always possible to decompose a basic hexahedral element into 3-Pyramid element, 2-Prism elements, 6-Tetra hedral elements and offcourse Hex is there as always.

So this means that it is always possible to create different kind of meshes using a Basic Hex mesh element. In MATLAB it is very easy to make a hex mesh u can follow these simple steps and u will get a Hex mesh.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x = [0:1/numx:1];
y = [0:1/numy:1];
z = [0:1/numz:1];

%Where numx, numy and numz are the number of basic hex elements u want in x, y and z %Direction.

%then follow the following step

[X Y Z] = meshgrid(x,y,z);

X = X(:);Y=Y(:);Z=Z(:);
%and then to plot the mesh you need following lines of code

node = [X Y Z];

figure(1);

if sloped==1
patch('Vertices',node,'Faces',faces,...
'FaceVertexCData',hsv(1),'FaceColor','none')
else
patch('Vertices',node,'Faces',faces,...
'FaceVertexCData',hsv(1),'FaceColor','none')
end
view(3); axis square

title(['Cartesian Mesh ', num2str(numx,3),'x',num2str(numy,3),'x',num2str(numz,3)])

% Now here one thing which you need to Compute is the Face connectivites which shoud %be fed into the function Patch which basically patches the different faces of the %hex and there by makes a complete Hexa Hedra. Now to get the Face connectivties you %need to use the following piece of code.

function faces = face_connectivity(num_u,num_v,num_w)


numx = num_u;
numy = num_v;
numz = num_w;

nnodex = numx+1;
nnodey = numy+1;
nnodez = numz+1;

face_pattern = [1 2 nnodex+2 nnodex+1]; % This is your face connectivity Pattern

nnx = numx+1 ;
nny = (nnodex)*(nnodey) ;
inc_u = 1;
inc_v = nnx;
inc_w = nny;
node_pattern=[ 1 2 nnx+2 nnx+1 nny+1 nny+2 nny+nnx+2 nny+nnx+1 ]; % Node connectivity
element = zeros(numx*numy*numz,8);
element = make_elem_hexa(node_pattern,numx,numy,numz,inc_u,inc_v,inc_w,nnx);

% ThisFunction gives the element connectivity.

faces = zeros(1,4);
face = zeros(6,4);
face1 = [1 2 3 4];
face2 = [4 3 7 8];
face3 = [5 6 7 8];
face4 = [2 6 7 3];
face5 = [1 5 8 4];
face6 = [1 2 6 5];

[m,n] = size(element);

for i = 1:size(element,1)

face = [element(i,face1);element(i,face2);element(i,face3);element(i,face4);element(i,face5);element(i,face6)];
faces = cat(1,faces,face);
end

faces(1,:) = [];
faces = faces;

Meshing Software Links

Hi,

This post will list most of the mesh generaiton software which are available in matlab and have features to generate delaunay meshes in 2 and 3 dimensions. Also I am going to list some other general mesh generators written in C++ and Fortran.

Matlab Mesh Generation :

1.) For General meshes in 2d and 3d check www.mayurpal.com.
2.) Simple Mesh generator in matlab by Per-Olof Persson.

3.) Another Matlab one.

4.) other realted link for Meshes in 2 and 3D in other languages.

I will be posting more stuff sooner for meshes in matlab.

Mesh Generation using Matlab

These days most of the research in the field of fluids, structures, porous media, brain computer interfacing you name it, uses numerical simulations. Reason: It is much cheaper and many times faster compared to experiments. Mesh Generation forms an integral part of numerical analysis/simulation. Although, there are plenty of commercial softwares based on Finite Element Methods and Finite Volume Methods like COMSOL, FLEUNT, ANSYS, NUMECA and many more with exceptional Mesh/Grid Generation features. But many times its difficult to use the meshes generated by these softwares which suits to your particluar simulation need. Reason: Many of the exsiting software don't have this feature where you can create a mesh and use it some which have such feathures requires you to do some complicated modifications in your code to import these meshes. There are although loads of mesh generator available some of which open source and free to download. But, then again problem comes does these free source code suits your purpose. I encountred this problem over the last couple of months. I am doing research in the field of Petroleum Reservoir Simulation and I need to test a lot of numerical examples on different sorts of meshes/grids in 2 and 3D. I do most of my simulation work in MATLAB, some people might argue that MATLAB is slow and all sorts of reason about other programming languages are faster like C++ and Fortran. I dont deny that fact but on the other hand the library of exsiting function which matlab has is amazing and its Array handling feature and sprase code it amazing too. The only and important reason I use MATLAB is its capability to handle array operations. In my simulation code I have to solve at times 9 simulatneous equations in 2D and 27 equations in 3D, which maximizes use of array operations. I also frequently use MAPLE to do my algebra and other good thing about MATLAB is that I can directly import the MAPLE algebra in Array Format into MATLAB which suits my purpose.

Now comming to the meshes in MATLAB, try doing a google on 'meshes in MATLAB' or 'grid generation in 2 and 3D in MATLAB', a invested a lot of time to find some unseful source code in matlab searching on google groups etc the only useful package I found was by Per-Olof Persson titled 'DistMesh - A Simple Mesh Generator in MATLAB'. No doubt its an amazing piece of work but again it didnt realy suits my purpose. The reason being I needed unstructured meshes of different element types in 3D like prisms, hex, tetra and pyramids. In 2D also I needed meshes which are boundary aligned to control volume and are matching to the underlying medium. So, What next ? I started from scratch and now I have come up with stand alone code in MATLAB which has functionality to create different kind of meshes in 2D and 3D. These are structured and Unstructured meshes, perturbed and bondary aligned too. If any one is in need of such meshes in 2 and 3D please have a look at www.mayurpal.com. Then you can drop me an email and I will get back to you and will help you and if required will also provide you with the source code if it suits your purpose.